Superb Owl

Phase Blindness

Our felt experience of time is thicker, weirder, and more malleable than you might think

I’d like to share one of my first (sober) mystical experiences. Unfortunately, it involves Joe Rogan.

I saw this video, and the secrets of the universe were revealed:

In one instant, I felt the immanent truth of Nietzsche’s eternal return. I could see the mechanism of karma itself. I understood immediately that every ostensibly unique experience is composed from an alphabet of smaller, not-unique-at-all experiences. That we are the echoes of patterns put in place long before us.

That description of the world may or may not actually be true. It was a mystical experience, not an intellectual epiphany. It was my visceral, felt sense of time that shifted in that moment—all the connections to Nietzsche and Hinduism fell out afterward, as I tried to make sense of it.

There are two things I’ve realized since:

• First: there’s a very elegant mathematical description of that shift in time perception, which just so happens to be a foundational part of signal processing.

• Second: that shift is a key ingredient in most or all of my mystical experiences.

Outline

• Good Vibrations

• Frequency and Phase

• The Thickness of Time

• Zooming In and Out

• The Fourier Transform

• Thick Time and Mystical Experience

Subscribe now

Good Vibrations

There’s a point, at around 20 beats per second (i.e. 20Hz1), where a driving rhythm turns into a hum. You can hear it in the video below:

There’s something important happening at the transition point. Physically, nothing much2 has changed—packets of compressed air are are hitting your ear just a bit faster than they were a moment ago. But perceptually the story is quite different—what before was a series of events spread out in time is now a single constant tone.

And this isn’t just an auditory phenomenon. You can spot it visually too: the turning wheels of a car blur into a solid object at high speeds; solid colors are really electromagnetic vibrations (the only physical difference between red and purple is that purple vibrates faster). Even smell is hypothesized to be vibratory, and yet most of us perceive scent as an unmoving constant—those tiny molecular vibrations are required for perception, but not perceivable themselves.

It’s as though your brain’s clock speed maxes out at some point, and stops trying to discern the individual impulses of the input signal. But it knows something is there, so it smears all that wiggling into a single, solid object.

Frequency and Phase

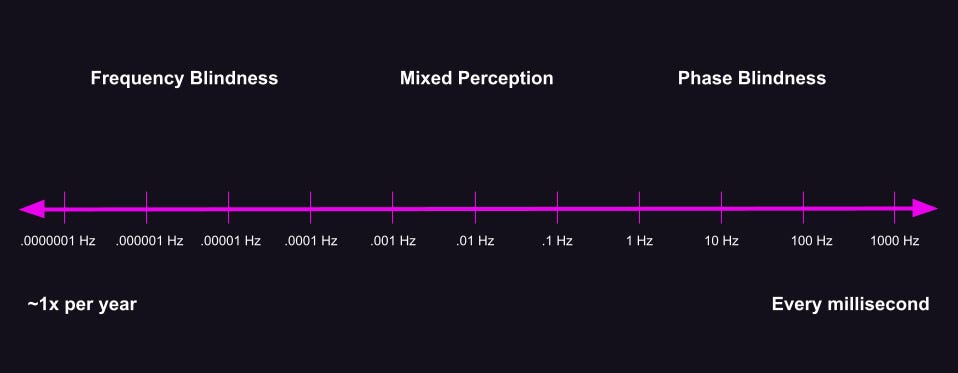
To be clear: it’s not an issue of your brain’s sampling rate being too low. The hum you hear when the rhythm exceeds 20Hz contains nearly all the information present in the original signal. There’s only one piece of information missing: the phase.

Frequency and phase (along with amplitude) are the most important variables in describing how a waveform evolves over time:

Some brief definitions:

• Amplitude: how high are the peaks, and how low are the valleys? Higher amplitude means bigger bumps.

• Frequency: how many peaks and valleys occur in a given time period? Higher frequency means more cycles per second.

• Phase: Are we currently3 at a peak, a valley, or somewhere in between? Unlike the other terms, higher phase doesn’t lead in one direction. Instead, phase is cyclic—if we start at a peak, and keep shifting the phase to the right, we come back to another peak.

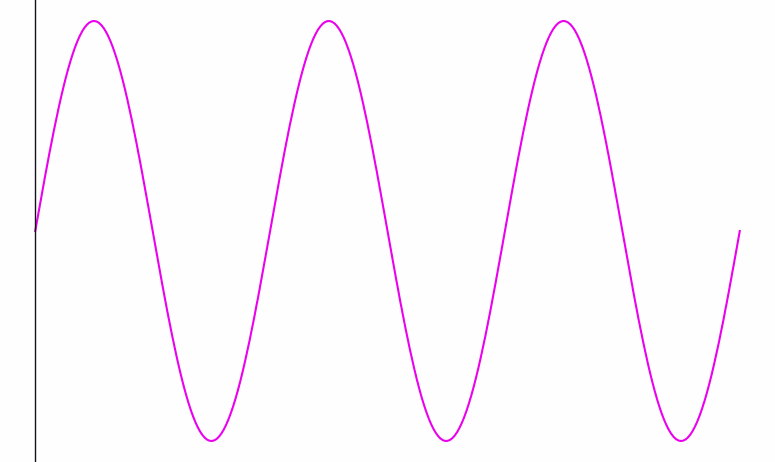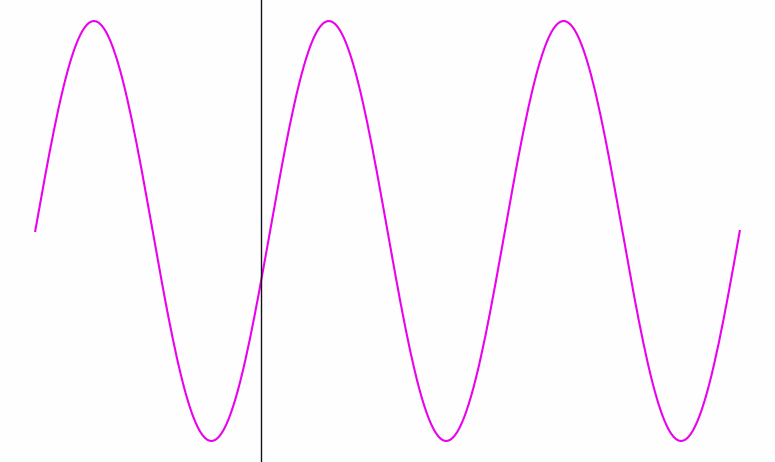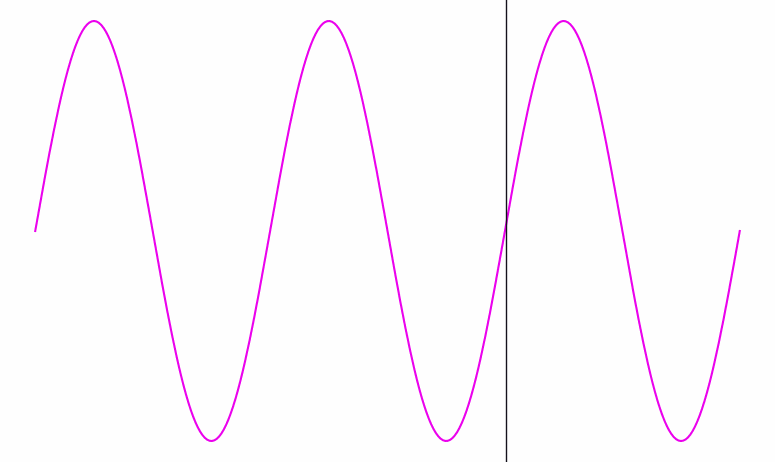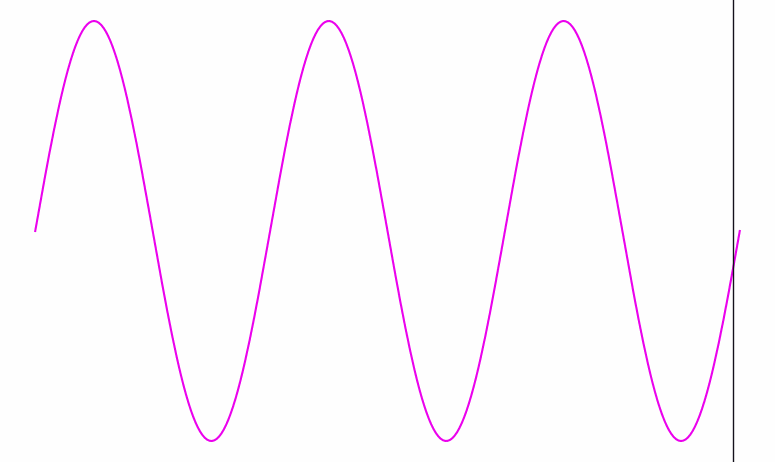
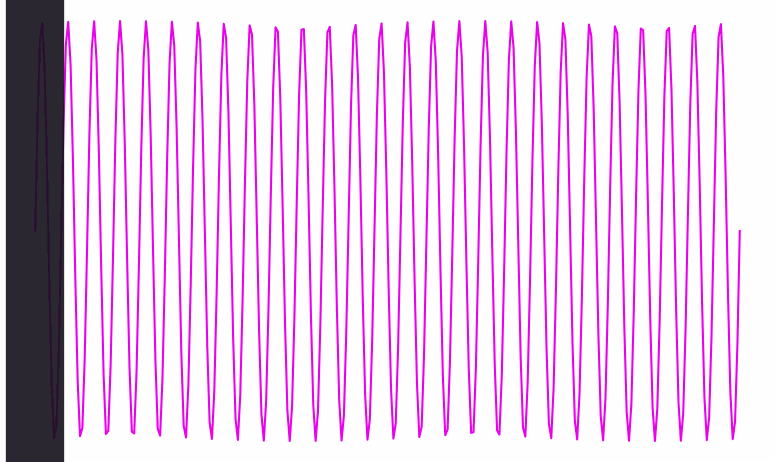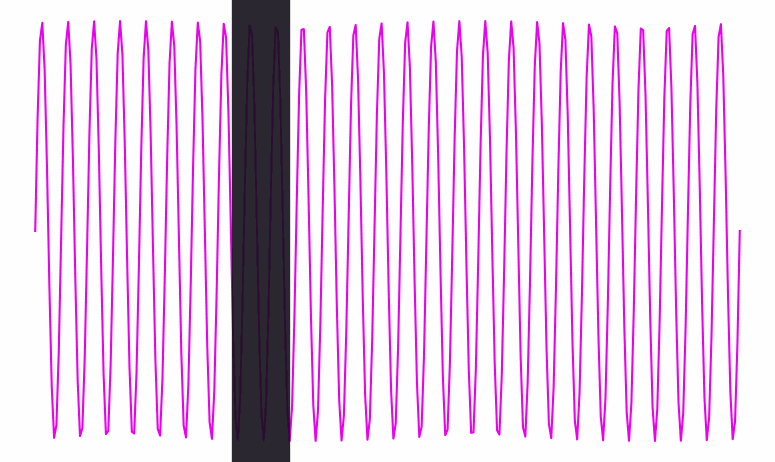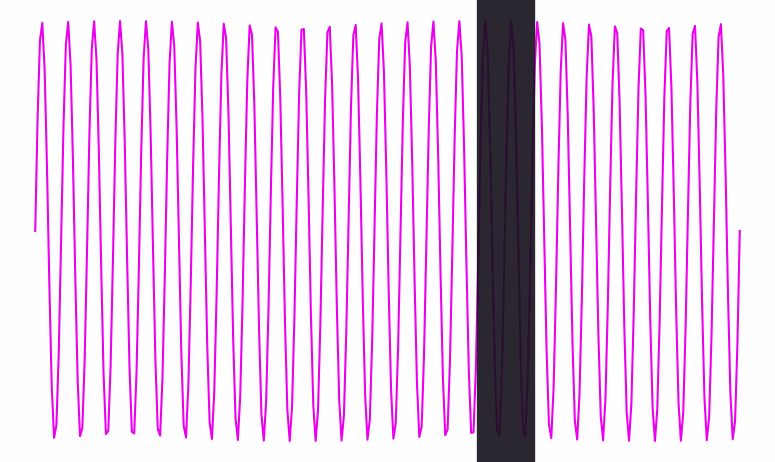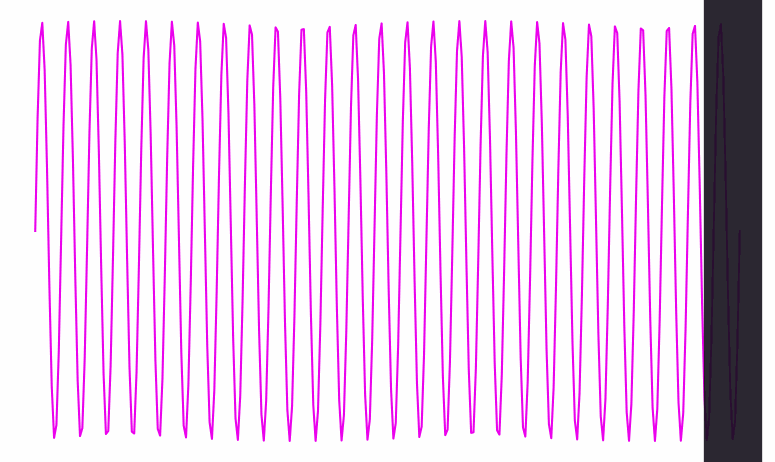
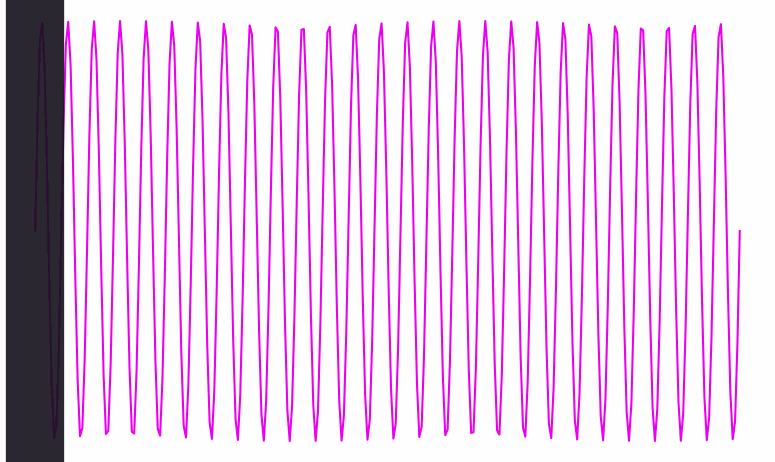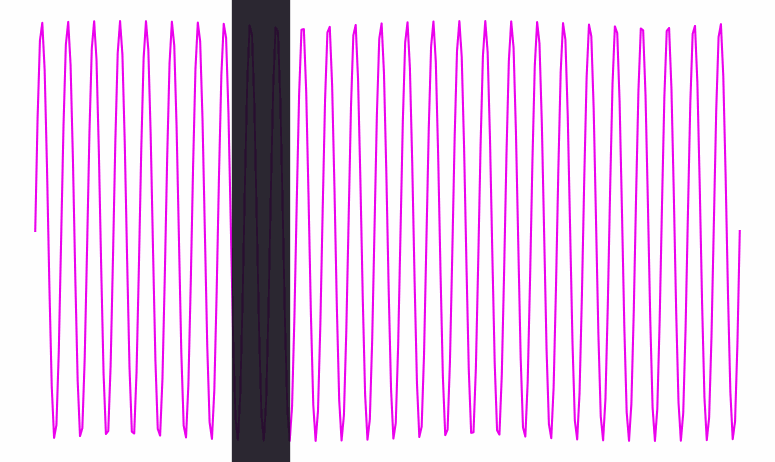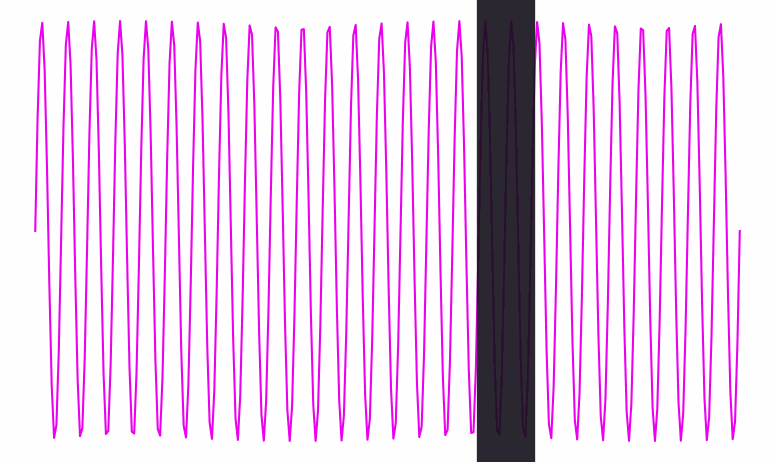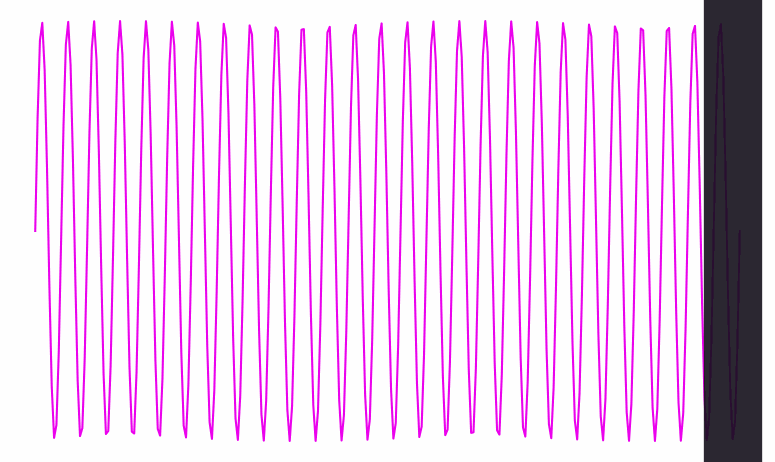
Here’s a visualization of a wave signal being processed. At each point in time, you can see the wave’s phase clearly—you can tell if we’re at a peak, a trough, or somewhere in between:

When the wave gets a lot faster (i.e. its frequency goes up), it becomes harder to see the beats. Eventually, they get so close together that they’re thinner than the width of the black line traversing them:

Inside that black bar, we can see the frequency of the wave inside it. But there’s no clearly defined phase; the bar doesn’t have any particular location among the wave’s crests and dips; it contains several of both.

Conversely, when the frequency is slow and spread out as in the first animation, the bar knows exactly where it is phase-wise. But from the bar’s perspective, it’s hard to see the wave’s frequency—it’s only seeing one tiny bit of the wave at a time.

So there’s a dual relationship between phase and frequency. When the waves are spread out, the bar captures phase, but not frequency; when the waves are packed in tight, the bar captures frequency, but not phase.

The Thickness of Time

That bar is a representation of how we experience time.

Following Husserl, let’s call it the thickness of the present moment. Our conscious experience is extended in time, so that there’s no precise, discrete notion of “now”. Here’s William James describing the phenomenon (emphasis mine):

In short, the practically cognized present is no knife-edge, but a saddle-back, with a certain breadth of its own…We do not first feel one end and then feel the other after it, and from the perception of the succession infer an interval of time between, but we seem to feel the interval of time as a whole

(There’s a physical basis for this thickness, which falls out of relativity. Your present moment is created by many different parts of your brain activating together. But information can’t travel faster than light—those different parts of your brain need time to cohere together. If an experience is spread out in space, it must also be spread out in time.)

Because of this thickness, we experience the same tradeoff we saw above with the black bar. Events that occur very rapidly smear together, and we lose track of phase, like in the video above where the rhythm gets too fast to hear the individual hits.

Conversely, events that occur far apart feel disconnected, even when they’re not. You might call this the thinness of the present moment—slow a rhythm down enough (below about 0.5Hz, or one hit every two seconds) and it no longer feels like rhythm. We hear sudden, random noises instead of the beat’s gestalt:

Zooming In and Out

Subscribe now

Interestingly, we seem to have some control over how thick our present is. We can expand and contract that time window at will.

I can deliberately zoom into the present moment, and feel all the individual events it comprises. This is actually a common meditation technique. For example, Daniel Ingram encourages his readers to see how many sensations they can count per second, aiming for around 10. It’s an exercise that helps us see what perception is like on the smallest scales, how it operates and evolves from moment to moment.

I can also zoom out, and see the present moment not as a unique event, but as the resonant residue of thousands of long-range patterns. I’m sitting here writing, because I have an established habit of writing. I’m doing so in my favorite coffee shop, having ordered my usual breakfast. Around me there’s a first date, a young woman reading a novel, and an older man on his laptop—all traditional coffee shop rituals, iterated into the present moment. Today is identical to a thousand other Sundays, this coffee shop identical to a thousand other coffee shops, modulo some minor details. When my perception of time shifts, like it did when watching that Joe Rogan video, the details completely fade into the background, and all I can see is repetition.

A lot of techniques (like Daniel’s) focus on the former, on how to clench and strengthen that attentional muscle. But relaxing it is just as important, if not moreso. Our natural state is one of narrowly focused attention—even if the direction of its gaze wanders capriciously. Relaxing into wide attention is crucial for recognizing and appreciating beauty. For me, clenching only leads to mystical experience when that muscle becomes so exhausted that it collapses.

Our hardware probably sets hard boundaries on how thin that band can get, putting a lower bound on phase perception. Sub-millisecond phase perception is probably out of the question—imagine being able to notice thousands of things per second!

Long time intervals, on the other hand, are probably limited not by hardware, but by lifespan. If I zoom out enough, I can sense the turning of day and night, and the cycle of the seasons. As I get older, I’m even beginning to glimpse the generational patterns that play out over decades, but they’re very fuzzy. There’s no way I could sense e.g. the climatological cycles that play out over centuries—my lifetime only covers one small section of a single cycle.

Scientific instruments can augment us here, of course. We can “speed up” or “slow down” time by taking measurements and plotting them on a graph that fits neatly on a page of paper, where we can see the signal indirectly. But there are hard lower and upper bounds on what we can experience viscerally.

Fortunately, there’s also a rich space in the middle, between milliseconds and years, where we can take either perspective, contracting or expanding the thickness of our present moment at will.

The Fourier Transform

Here’s what happens mathematically when you unclench that attentional muscle and let your time window expand:

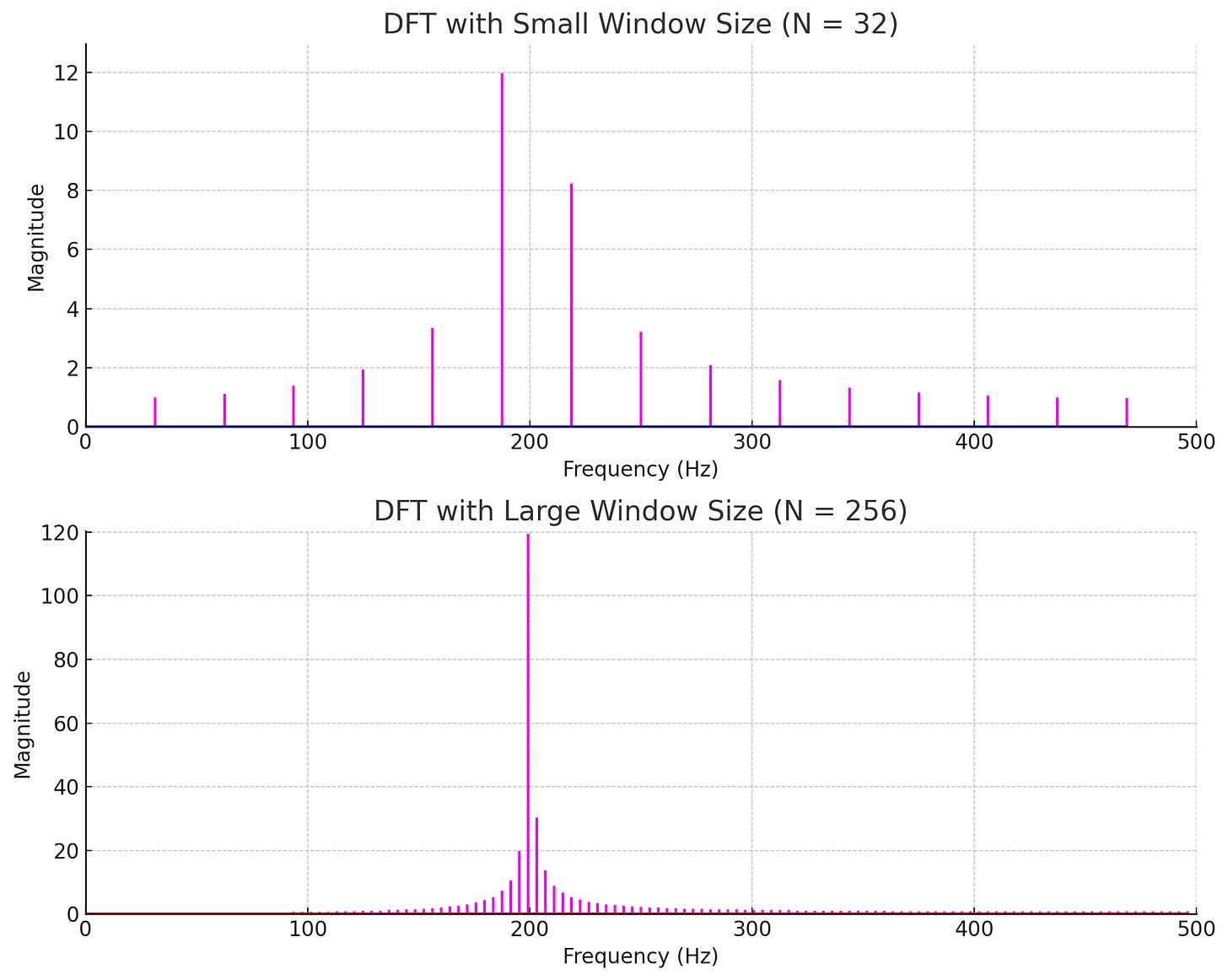
These are both Fourier transforms of the same sine wave—but the second one uses a much larger window, giving it a much clearer picture of the wave’s frequency.

The Fourier transform is a beautiful4 mathematical procedure that let’s us see a signal from either perspective: in terms of phase/rhythm/events, or in terms of frequency/tone/patterns. We call the former the “time domain”, and it’s how you’re probably used to looking at sine waves (with time on the x-axis and intensity on the y-axis). The latter is called the “frequency domain”—frequency is on the x-axis, and intensity on the y-axis. The Fourier transform is a way of shifting between these two perspectives.5

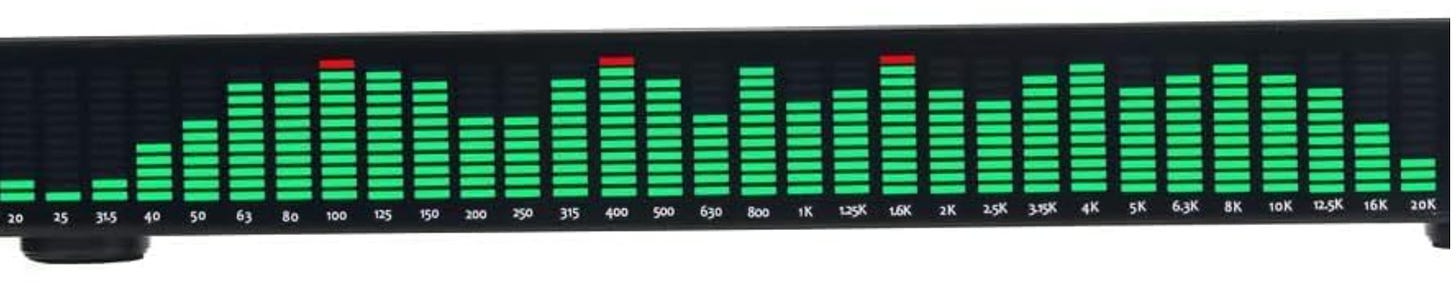
So if the original signal is a sine wave vibrating at 200Hz, its Fourier transform will just show a vertical bar at 200. If the wave is more complicated, with many frequencies mixed together, you’ll see more vertical bars, with taller bars for stronger frequencies. If it’s white noise, you’ll see nothing but a block of equally-sized vertical bars.

You need the whole signal to accurately compute its Fourier transform. But usually we want to process a signal in real time—we can’t wait for the whole signal to arrive before we start analyzing it. The solution is to use a “sliding window”—we perform many Fourier transforms, one small chunk at a time.

Again, as the band gets wider, we capture more of the signal, so our picture of the frequency gets clearer (and our picture of the phase gets fuzzier6). The resulting Fourier transform gets better and better at approximating the “true” Fourier transform of the full signal.

The example at the top of this section shows two Fourier transforms with different window sizes. The original signal is just a sine wave vibrating at 200Hz—so the “true” Fourier transform should just be a vertical line at 200. With a narrow window, we can sort of see a peak near 200, but there’s a lot of other noise there; with a larger window, the picture becomes much sharper. With an infinitely large window, we’d get the pure form of a vertical line at 200.

Thick Time and Mystical Experience

There’s a meditation exercise I enjoy, where I progressively thicken my experience of time. I start by focusing on the present moment, plus or minus a second or two. Then I expand the error bars, thinking about today, then about this week, this month. Eventually I’m considering the trajectory of my life over the past and coming years, and finally seeing my life as a cohesive whole.

I’ve had a handful of moments, on and off psychedelics, where I zoom out completely. It feels like I can see the whole universe at once, Alpha and Omega. The picture might be a little fuzzy, but it’s all there.

I can’t say this is a true revelation, because I’ve never come back with new information—I can’t suddenly predict the future. But that’s precisely what we’d expect with the Fourier transform. It doesn’t add or remove information—it rearranges existing information to provide a new perspective. The shift I’m experiencing isn’t some download of information from the Akashic records, it’s a birds eye view of all my memories and experiences, my life splayed out before me as a fixed pattern in space rather than a moving pattern in time. “My life flashed before my eyes,” mathematically stated, is “I saw the Fourier transform of my life.”

There are simpler—but equally profound—experiences to be had as well. Zooming in instead of out can lead to an absorption in the present moment, which counterintuitively delivers the same felt sense of eternity.

For me, this tends to happen when the present moment is highly repetitive, and the thinking mind has faded into the background. Sitting quietly with birds chirping and branches waving in the wind, I start to forget that there was a time before this, or that there will be a time after; there is only breath, birds, branches, repeating forever. And I can see all of it at once.

In both cases, the Fourier window extends over the entire signal available to my thinking mind. In the former case, where my mind is active and capable of considering things like the big bang and heat death, the Fourier window has to swell up to cosmic proportions (or more practically, to cover every experience I’ve had since birth). In the latter case, where my mind is quiet, the Fourier window only has to cover a few seconds.

(Generally I would suggest the latter—it’s a lot easier to get there, and less likely to lead to psychosis.)

Again, I can’t tell you if what I’m seeing in these moments points to some grander truth. But I can tell you that there is an experience of time which is radically different from the norm, a shift in temporal perspective that transforms the world from an unfolding present into an eternal hum. And I love it.

Subscribe now

Share

PS: for a completely different (but compelling!) description of the experience of time, see QRI’s pseudo time arrow. If you have ideas on how to connect the two please leave a note in the comments.