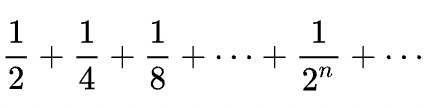Superb Owl

About | RSS | Substack | Twitter
Subscribe via Substack:

Church of Reality: Cantor on Infinity and Divine Freedom

Cantor uncovered the nature of infinity, but both mathematicians and theologians accused him of blasphemy.

View on Substack

This post is part of a series on the philosophical and spiritual views of prominent scientists and mathematicians. Past subjects include Erwin Schrödinger. Future subjects will include Albert Einstein, Werner Heisenberg, and Barbara McClintock.

Subscribe now

Georg Cantor is one of the most prominent mathematicians in the history of the field. He discovered a radical new vision of infinity, and his invention of Set Theory steered mathematics both into and out of its foundational crisis.

But Cantor was also a devout Lutheran. His mathematical ideas were deeply intertwined with his theology, and he believed he had been chosen by God to reveal the nature of the infinite to the world.

Cantor’s conception of infinity was deeply controversial with both mathematicians and the clergy. Let’s dig into his theory and see why.

Photograph of Cantor
It was tempting to use a picture of Buzz Lightyear instead.

Outline

Metaphysics and Mathematics

It may seem odd to discuss math and metaphysics in the same breath—the former is typically associated with sober logic, and the latter with unfalsifiable speculation. But in Cantor’s time, mathematics lacked a strong foundational underpinning; no one could agree on exactly what the rules were, and the debate hinged entirely on metaphysical assumptions.

At the time, there was a strong conservative party—known as the Constructivists—led by Leopold Kronecker. They believed that valid mathematical objects had to be constructed rigorously from existing objects (primarily the natural numbers 1, 2, 3, …), rather than invented ex nihilo. They were particularly skeptical of irrational numbers and the idea of infinity. As Kronecker famously stated:

Natural numbers were created by God, everything else is the work of men.

Cantor stood in total opposition to this: he believed that any consistent system of logic should be considered mathematics, regardless of how it relates to the natural numbers. In his essay Foundations of a General Theory of Sets (typically called his Grundlagen), Cantor takes a jab at Kronecker’s position:

…an opinion is frequently presented concerning the essence and meaning of numerical magnitudes, according to which no numbers can be assumed as really existing other than the finite real whole numbers of our number-class (I).

At most the rational numbers which immediately spring from them are granted a certain reality. However, the irrational numbers supposedly have a merely formal significance in pure mathematics…all truths found in arithmetic and analysis, or still begging discovery, are presumably to be regarded as relationships among finite whole numbers

In opposition, he states:

Mathematics is entirely free in its development, bound only by the self-evident concern that its concepts be both internally without contradiction and stand in definite relations, organized by means of definitions, to previously formed, already existing and proven concepts…As soon as a number satisfies all these conditions, mathematics can and must regard it as existent and real. Here I see the reason…why the rational, irrational and complex numbers should be regarded just as much as existent as the finite positive whole numbers.

…the essence of mathematics lies precisely in its freedom.

These views were controversial, but ultimately Cantor won out, thanks to his creation of a powerful new infinity.

Infinity

Actual and Potential Infinity

Infinity is an old idea. Some of the earliest records go back to Indian and pre-Socratic Greek scholars, as early as the 4th Century BCE. But until Cantor, Western mathematics was pretty skeptical of the idea.

Aristotle began the debate over Actual versus Potential Infinity. The latter acknowledges that there are domains, like the natural numbers, where you can have “as many as you want,” but refuses to accept the idea of infinity as a number.

Mathematicians, led by the Constructivists, stuck to Aristotle’s dogma: infinitum actu non datur, ”The actual infinite does not exist.” For instance, the infinite sum

Sum of 1/2^n, starting at n=1

might have been said to “equal 1”—but this was understood to be shorthand for saying “with enough terms, the sum can surpass any number less than one.” That is, you give me any number less than one, like .9999999, and I can start counting off terms in the series above and be confident that, after some finite number of terms, I’ll have a number bigger than .9999999.

Does this sound unnecessarily complicated? It certainly did to Cantor.

Cantor’s Discovery

Counting gets weird when you start working with infinite sets. What’s the number of natural numbers? Infinity, naturally.

Cantor’s Set Theory made counting rigorous, even when dealing with infinite sets. To compare the number of things in set A with the number of things in set B, we see if we can put them in a one-to-one mapping. If we can, they must have the same number.

This is a little bit simpler than counting both sets, and it obviously behaves as expected for finite sets. But things get weird for infinite sets. For instance: there are just as many even numbers as there are numbers!

Bijection between the natural numbers and the even numbers
You’d think removing odd numbers would leave you with fewer numbers, but not according to Set Theory

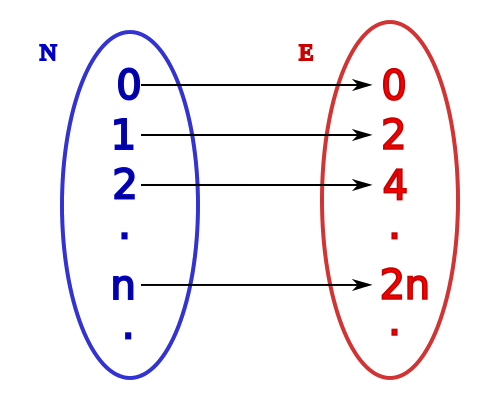
But despite some counterintuitive examples, this method of counting has been widely accepted in mathematics. And it’s exactly what leads to Cantor’s brilliant leap forward: he proved that there’s no way to get a one-to-one mapping between the natural numbers and the real numbers—you’ll always have some real numbers left over. There are an infinite number of natural numbers, but an even bigger infinite number of reals!

I’ll avoid reconstructing the full proof here, but it’s fairly easy to follow, even for non-mathematicians. Wikipedia does a good job of explaining.

What’s more, the same technique can be used to create an infinite number of ever-larger infinities. This section of the Grundlagen reads like an academic version of escalating playground taunts: well you’re stupid times infinity plus a hundred!

At the time, Cantor’s description of infinity was wildly controversial. Kronecker, Poincaré, Weyl, and Wittgenstein all voiced their dissent, often with an outrageous level of derision: the first called him a “charlatan” and the last said his ideas were “utter nonsense.” But today, Cantor’s proof has been completely absorbed into mathematics, and is taught as part of any undergraduate curriculum.

Freedom and Heresy

Cantor’s anti-Constructivist approach to mathematics wasn’t simply a post-hoc defense of his infinity; it was the result of years of philosophical thought and research. But his beliefs continued to evolve over the course of his career.

Subscribe now

Mathematical and Divine Freedom

In the Grundlagen, Cantor begins his defense of mathematical freedom by asserting his belief in the Principle of Plenitude: that everything that can exist, does exist.

We can speak of the reality or the existence of the whole numbers, both the finite and infinite ones, in two senses…On the one hand we may regard the whole numbers as real insofar as they take up a very definite place in our mind…Let me call this type of reality of our numbers their intrasubjective or immanent reality. Then again we can ascribe reality to numbers insofar as they must be regarded as an expression or image of occurrences and relationships in the external world…This second type of reality I call the transsubjective or transient reality…

Given the thoroughly realist—simultaneously, however, no less idealist—foundation of my investigations, there is no doubt in my mind that these two types of reality will always be found together, in the sense that a concept to be regarded as existent in the first respect will always in certain, even in infinitely many ways, possess a transient reality as well….

It’s from here that Cantor launches into his defense of mathematical freedom:

This coherence is referred to here in order to deduce from it what appears to me to be a most important consequence for mathematics, namely that mathematics in the shaping of its conceptual material need take into account solely and uniquely the immanent reality of its concepts and thus is under no obligation whatsoever to also test these concepts with respect to their transient reality.

But interestingly, he later repudiates the Principle of Plenitude in a correspondence with Cardinal Johann Franzelin, after the Cardinal accuses him of pantheism. The issue is that, in establishing mathematical freedom, Cantor has denied God’s freedom! By stating that every immanent reality by necessity comes into being as a transient reality (i.e. as a part of creation), Cantor has denied God’s omnipotence.

After the Cardinal points out this apparent error in judgement, Cantor immediately recants:

It was not my intention, in the passage in question, to speak of an objective, metaphysical necessity in the creative act, a necessity that would subjugate God’s absolute freedom.

And this was not simply for the Cardinal’s benefit. In a later letter to Bishop Ebhard Illigens, he writes:

Consequently I call the being concerned a “possible” being. By this is not meant that the being somewhere, somehow and sometime exists in actuality.

He defends his original idea in a weaker form, saying that consistency only implies an idea is realizable, not that it’s realized:

If I have recognised the inner consistency of a concept which points to a being, then the idea of God’s omnipotence impels me to think of the being as expressed by the concept as in some way actually realizable.

Transfinitude

But Cantor still had another issue of dogma to contend with: the orthodoxy of the time equated infinity with God. Placing infinity within the realm of mathematics, where it can be symbolically manipulated and reasoned about, would have subordinated God to logic.

So Cantor began to refer to his numbers as “transfinite,” rather than “infinite.” He broke infinity down into three categories:

In a letter to David Hilbert, Cantor says:

I have no doubt that, as we pursue this path [of generating numbers] even further, we shall never reach a boundary that cannot be crossed; but that we shall also never achieve even an approximate conception of the absolute. The absolute can only be acknowledged [anerkannt] but never known [erkannt]—and not even approximately known.

In the letters with Cardinal Franzelin, as he’s honing a dogma-friendly version of his argument, he even describes the transfinite numbers as a proof of God:

The Transfinite with its abundance of formations and forms, points with necessity to an Absolute, to the "truly Infinite," to whose Magnitude nothing can be added or subtracted and which therefore is to be seen quantitatively as absolute Maximum. The latter exceeds, so to speak, the human power of comprehension and eludes particularly mathematical determination; whereas the Transfinite not only fills the vast field of the possible in God's knowledge, but also offers a rich, constantly increasing field of ideal inquiry[.]

I find this schema quite beautiful: an ever-increasing collection of transfinite numbers, ultimately bounded by an inconceivable Absolute. The infinite ladder of infinities devised by Cantor can be quite dizzying; placing the Absolute back into the picture helps us reorient. Truly a paradise, to use Hilbert’s description.

The Art of Metaphysics

It would be easy to look at Cantor’s philosophical squirming as a sign of moral weakness. We tend to champion the renegade scientists and mathematicians who stand up to orthodoxy in order to propagate a more sensible world view. Cantor’s capitulation to the Cardinal looks weak next to Galileo’s eppur si muove.

But I think this would be short-sighted. Cantor was clearly willing to take on the mathematical establishment; why not the religious one? It’s possible that Cantor was simply desperate for validation after being rejected by his mathematical contemporaries, or that his Lutheran upbringing left him with a chronic fear of blaspheming. But regardless of his motivations, I see something beautiful in Cantor’s philosophical evolution.

Great art needs constraints. The revelation of modern art was not that we can do away with all constraints (unless you’re John Cage), but that we can choose our constraints. And so you get Warhol’s silk screens, Mondrian’s lines, Steve Reich’s loops. Classical art is different in that it adheres to rigid constraints with long histories, like those of symphonies and sonnets.

The beauty and difficulty in modern metaphysics is that, like modern art, it is completely unmoored—there are no constraints beyond logic itself, which is a bit like saying music has to make sound. Philosophers of metaphysics can choose any particular system to work within, or construct their own, much like a modern artist.

Cantor was simply a classical metaphysician, working within an established tradition and helping to further it along. And if we take him at his word, we have that tradition to thank for his astounding mathematical vision.

Sources

Primary

Secondary

Join the discussion on Substack!